¿Sabías que una simple pizza puede ayudarte a entender las matemáticas? Las gráficas circulares o de pastel son una excelente forma de representar datos de manera clara y visual. Acompáñanos en esta entrada para descubrir cómo se usan y cómo puedes crear las tuyas.
📘 ¿Qué es una gráfica circular?
Una gráfica circular es una representación en forma de círculo que se divide en sectores (o “rebanadas”) según la proporción de los datos. Cada sector representa una frecuencia absoluta, es decir, cuántas veces se repite un dato.
🔵 El círculo completo equivale a 360°, por lo tanto, cada dato se convierte en un ángulo proporcional.
📐 ¿Cómo calcular los grados de cada sector?
Usamos la siguiente fórmula:
Grados=(360°/Totaldedatos)×Frecuenciadeldato
Esta operación nos dice cuántos grados del círculo se deben asignar a cada categoría.
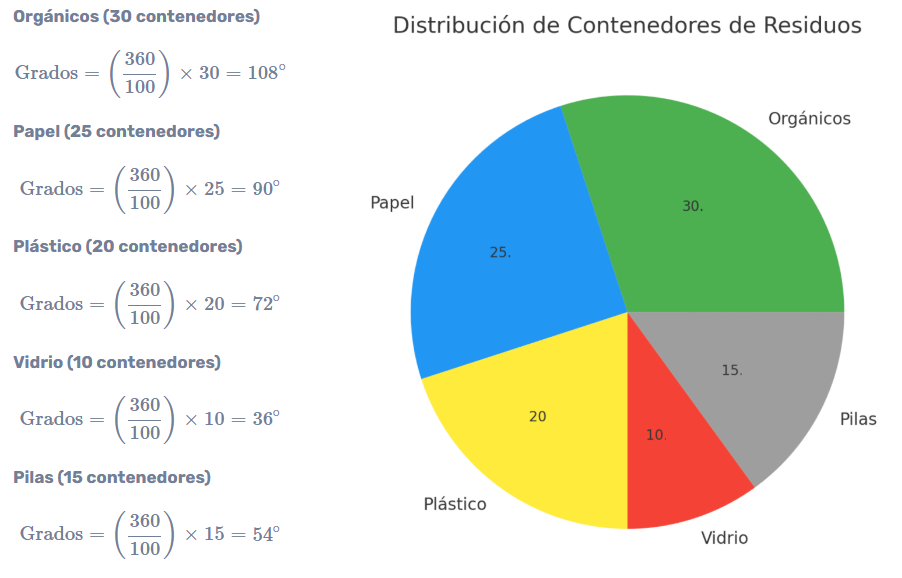
📊 Ejemplo 1: Reciclaje
Una empresa instaló 100 contenedores para reciclar distintos tipos de residuos. La distribución fue:
| Residuo | Cantidad | Grados |
|---|---|---|
| Orgánicos | 30 | 108° |
| Papel | 25 | 90° |
| Plástico | 20 | 72° |
| Vidrio | 10 | 36° |
| Pilas | 15 | 54° |
Cálculo de Grados para Cada Tipo de Residuo
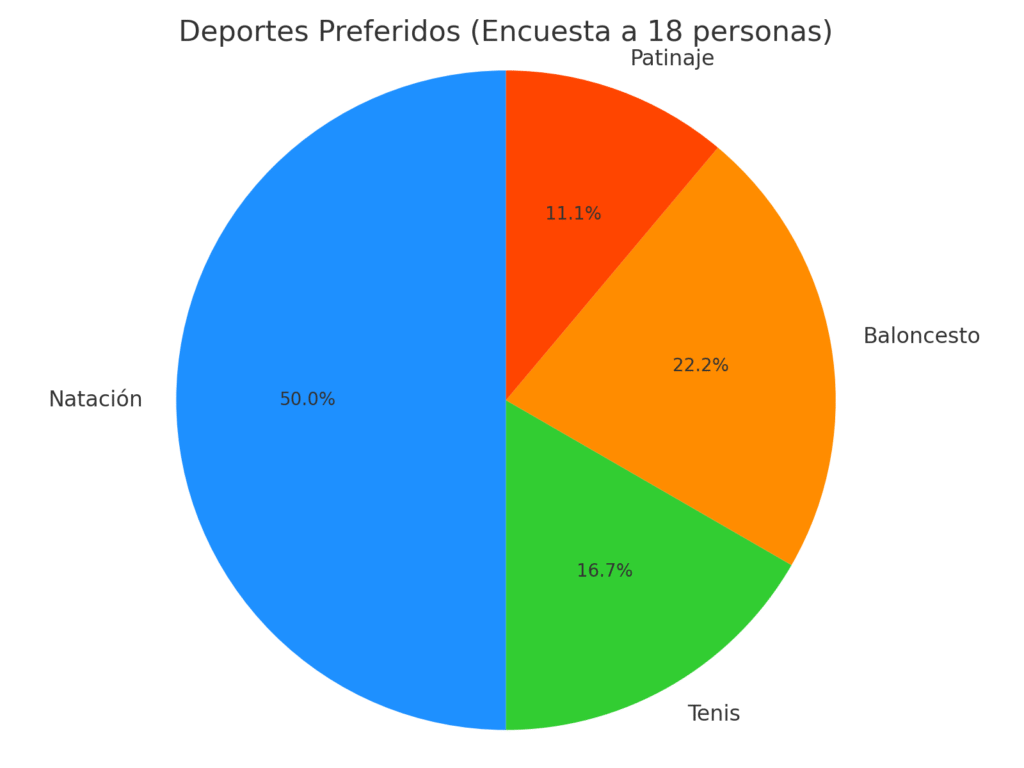
🧮 Ejemplo 2: Deportes preferidos
Se preguntó a 18 personas cuál era su deporte favorito. Los resultados fueron:
| Deporte preferido | Cantidad de personas |
|---|---|
| Natación | 9 |
| Tenis | 3 |
| Baloncesto | 4 |
| Patinaje | 2 |
Veamos los cálculos para cada uno:
- Natación: (360 / 18) × 9 = 180°
- Tenis: (360 / 18) × 3 = 60°
- Baloncesto: (360 / 18) × 4 = 80°
- Patinaje: (360 / 18) × 2 = 40°
Cada valor se traduce en una porción del círculo que representa con exactitud la proporción de personas que eligieron ese deporte.
🧠 ¿Dónde vemos estas gráficas en la vida real?
- Noticias y reportes
- Resultados de encuestas
- Estadísticas escolares
- Distribución de gastos o presupuestos
Observar y entender gráficas circulares nos ayuda a tomar decisiones y analizar información de forma visual y rápida.
🎯 Conclusión
Las gráficas circulares nos permiten representar porcentajes y proporciones de una forma clara y llamativa. Aprender a leerlas y construirlas es una habilidad útil en matemáticas, ciencias y la vida cotidiana.
