¿Alguna vez te has preguntado cómo representar fracciones o decimales en una recta numérica? 🤔 ¡No te preocupes! Hoy aprenderás de manera fácil y rápida a ubicar números racionales (es decir, fracciones y decimales) en la recta numérica. ¡Vamos a ello! 🚀
¿Qué son los Números Racionales?
Los números racionales son aquellos que se pueden expresar como una fracción a/b, donde a y b son números enteros y b ≠ 0. Ejemplos:
- 1/2 (un medio)
- 0.75 (que es igual a 3/4)
- -2/3 (negativo dos tercios)
Pasos para Ubicar Números Racionales en la Recta Numérica
1️⃣ Identifica el intervalo:
- Si el número es positivo, estará a la derecha del 0.
- Si es negativo, estará a la izquierda del 0.
2️⃣ Divide la recta en partes iguales:
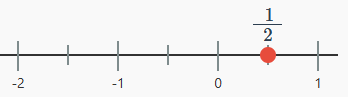
- Por ejemplo, si quieres ubicar 1/2, divide el espacio entre 0 y 1 en 2 partes iguales. El punto medio será 1/2.
3️⃣ Para fracciones impropias (mayores que 1):
- Convierte la fracción a número mixto.
- Ejemplo:
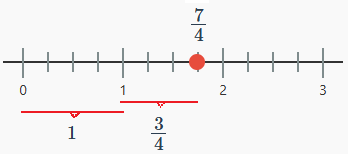
- \(\frac{7}{4} \) = 1 \(\frac{3}{4} \).
- Ubica el 1 y luego las tres cuartas partes entre 1 y 2.
4️⃣ Para decimales:
- Convierte el decimal a fracción si es necesario.
- Ejemplo: 0.6 = 6/10 = 3/5. Divide el espacio entre 0 y 1 en 5 partes y marca 3 de ellas.
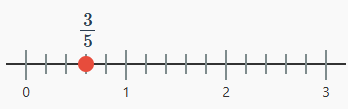
Ejemplo Visual 🎯
Imagina esta recta numérica:

- -1/2 está a la mitad entre -1 y 0.
- 3/2 (que es 1.5) está a la mitad entre 1 y 2.
¡Practiquemos! ✍️
Intenta ubicar estos números en una recta numérica:
✅ 2/3
✅ -0.5 (¿Sabes qué fracción representa?)
✅ 7/4
📌 Tip: Usa regla y colores para hacerlo más divertido. 🎨
¡Y eso es todo! Ahora ya sabes cómo representar números racionales en la recta numérica. ¿Fácil, verdad? 😊 Si tienes dudas, ¡déjalas en los comentarios! 👇