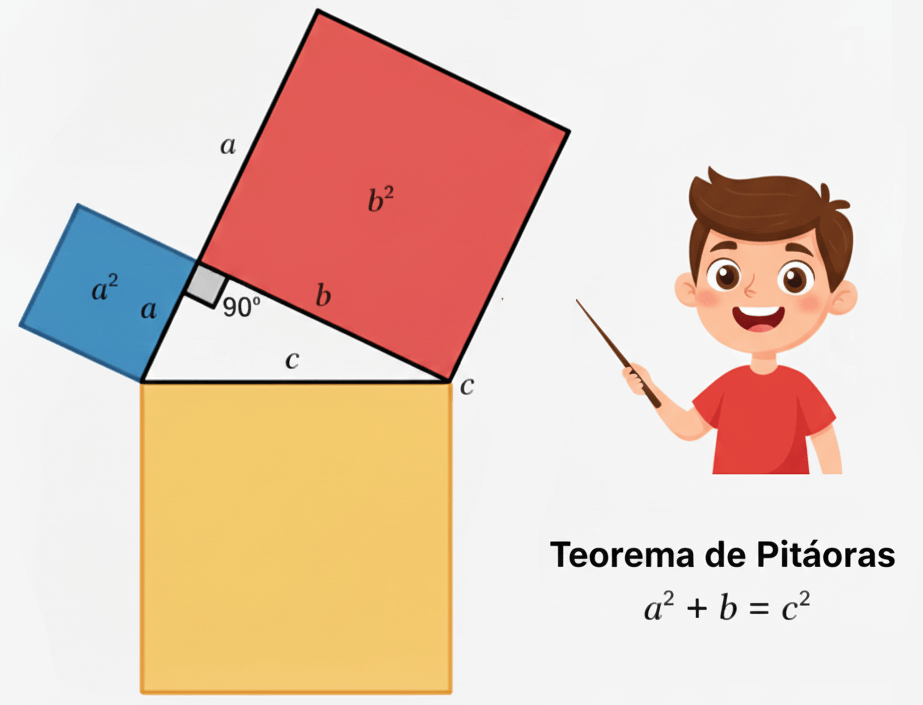
En la vida cotidiana, muchas veces necesitamos calcular distancias que no podemos medir directamente: la altura de un árbol, la longitud de una escalera apoyada en la pared o la distancia a la que observamos un objeto. Para resolver estos problemas existe una fórmula matemática muy especial: el Teorema de Pitágoras.
📘 ¿Qué dice el Teorema de Pitágoras?
En todo triángulo rectángulo, el cuadrado de la hipotenusa (el lado más largo, opuesto al ángulo recto) es igual a la suma de los cuadrados de los catetos (los otros dos lados).
\[ h^2 = a^2 + b^2 \]
Donde:
- h es la hipotenusa.
- a y b son los catetos.
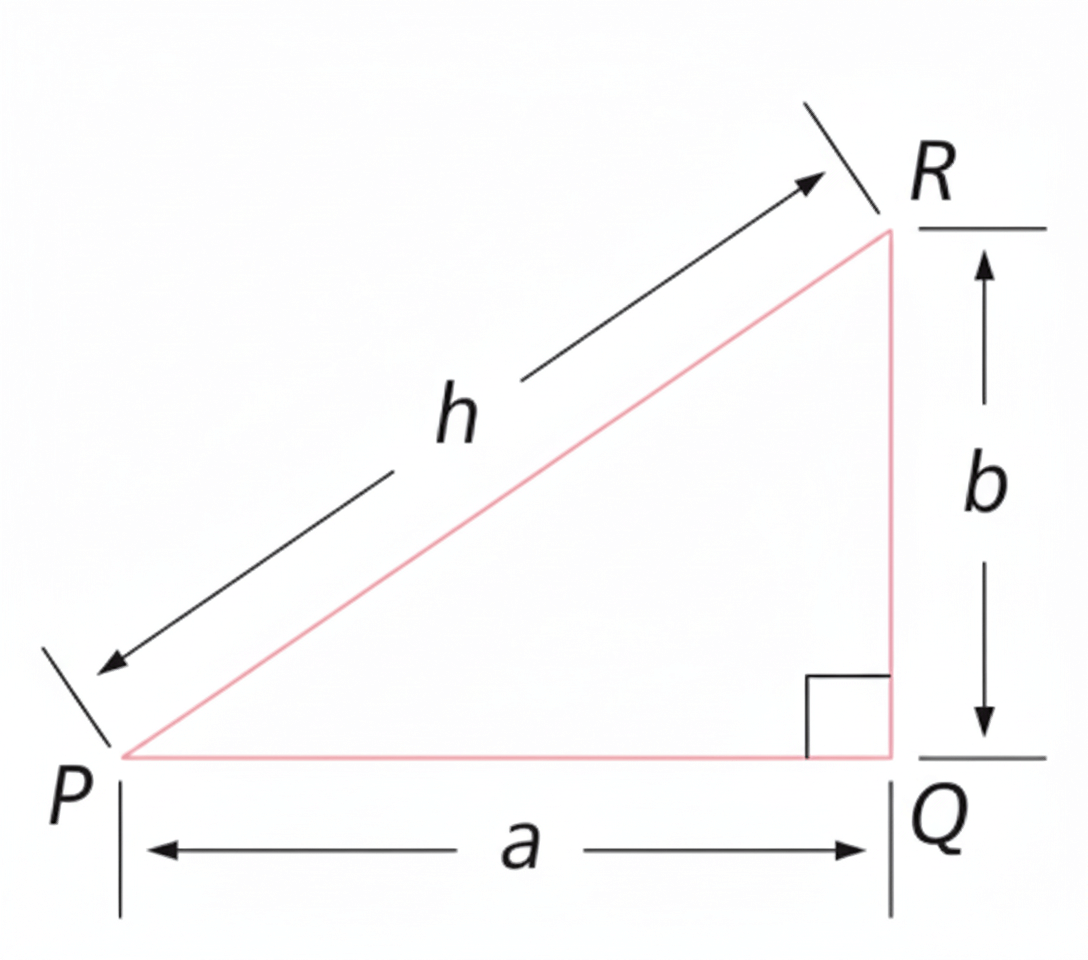
👀 Ejemplos prácticos
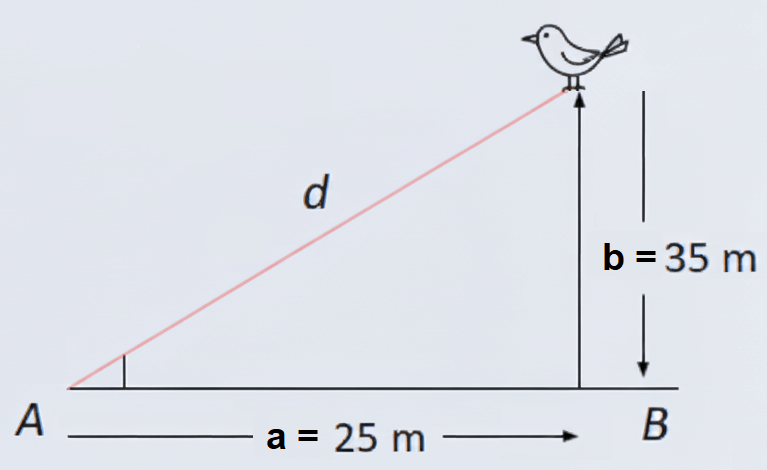
🔭 1. El telescopio de Andrés
Andrés observa un ave que está a 25 m de distancia horizontal y a 35 m de altura. Para saber la distancia real al ave, aplicamos el Teorema de Pitágoras:
\(
d^2 = 25^2 + 35^2
\)\(
d^2 = 625 + 1225 = 1850
\)\(
d^2 = 1850
\)\(
d = \sqrt{1850} \approx 43.01 \, m
\)Como su telescopio alcanza hasta 50 m, ¡sí podrá verla con detalle!
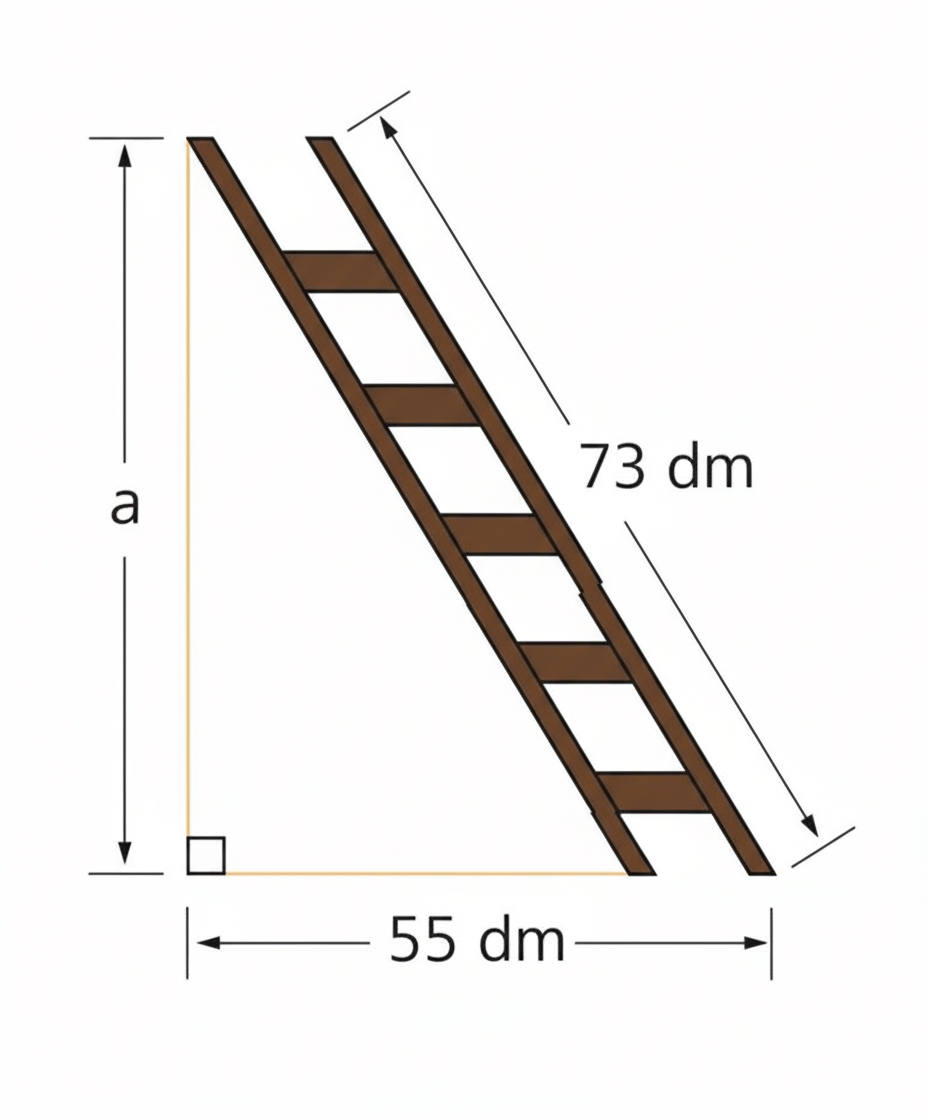
🪜 2. La escalera apoyada en la pared
Una escalera mide 73 dm y se apoya a 55 dm de la pared. ¿A qué altura llega?
\[
a^2 = 73^2 – 55^2 = 5329 – 3025 = 2304
\]\[
a = \sqrt{2304} = 48 \ dm
\]La escalera llega a una altura de 48 decímetros.
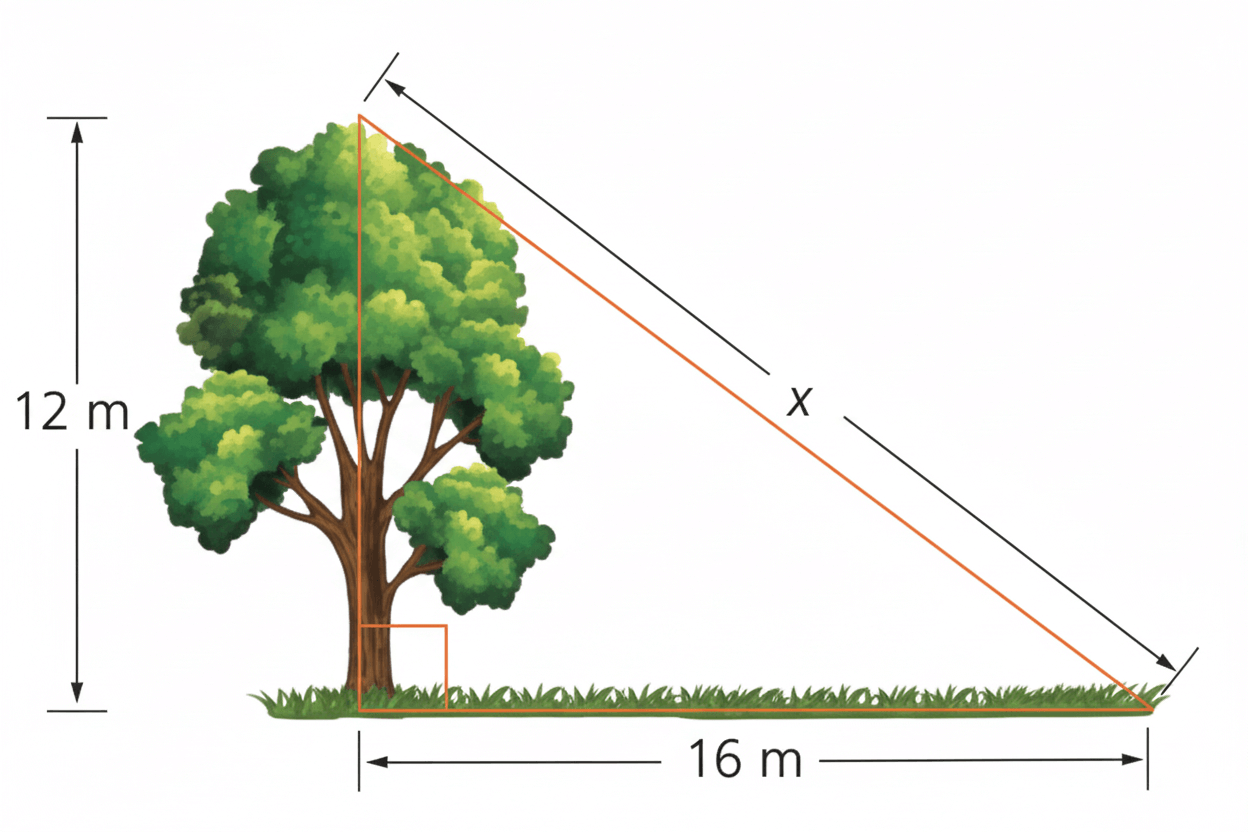
🌳 3. La sombra de un árbol
Un árbol mide 12 m y su sombra es de 16 m. La distancia desde la copa hasta el extremo de la sombra es:
\[
x^2 = 16^2 + 12^2 = 256 + 144 = 400
\]\[
x = \sqrt{400} = 20 \, m
\]Es decir, la copa y el extremo de la sombra están separados por 20 m.
🧩 Actividades de aprendizaje
- Calcula la diagonal de un cuadrado de lado 7 cm.
- Halla el radio de una circunferencia donde se inscribe un cuadrado de lado 9 dm.
- Resuelve problemas cotidianos, como la altura de un edificio visto desde cierta distancia.
✨ Conclusión
El Teorema de Pitágoras no solo es una fórmula matemática, sino una herramienta que nos permite medir lo que no podemos alcanzar directamente. Desde la antigüedad hasta hoy, sigue siendo una de las bases más importantes de la geometría.