En geometría, los movimientos en el plano son transformaciones que permiten desplazar, girar o reflejar figuras sin alterar su forma ni su tamaño. Estos movimientos mantienen la congruencia de las figuras y se utilizan en la vida cotidiana, en el arte, el diseño, la arquitectura y hasta en la naturaleza.
A continuación, exploraremos los tres principales movimientos en el plano: traslación, rotación y reflexión.
🔹 1. Traslación
La traslación consiste en mover una figura a lo largo de una línea recta, siguiendo una dirección y un sentido determinados por un vector.
- La figura conserva su forma y tamaño.
- Todos los puntos de la figura se desplazan la misma distancia y en la misma dirección.
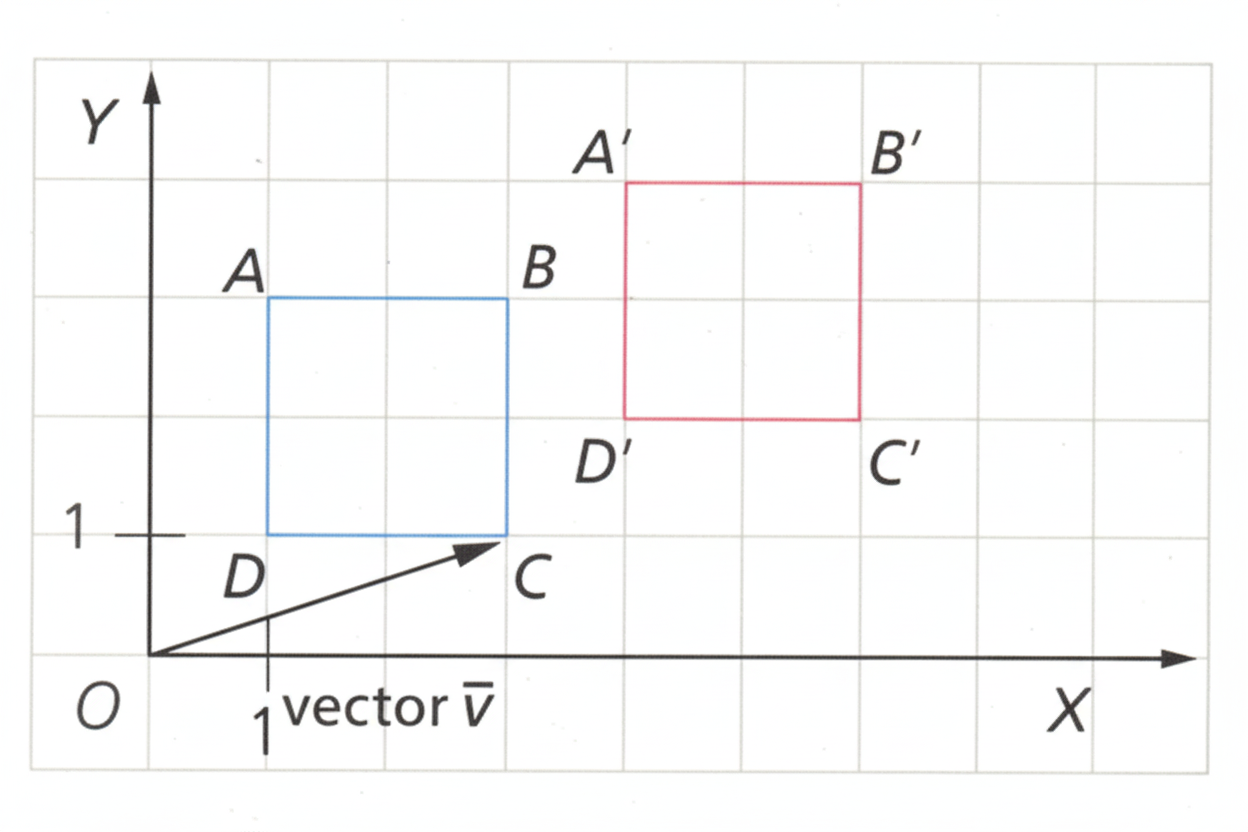
Ejemplo:
Si trasladamos un cuadrado hacia la derecha tres unidades y una unidad hacia arriba, cada vértice de la figura se moverá siguiendo ese mismo vector, obteniendo una copia idéntica de la figura en otra posición.
🔹 2. Rotación
La rotación es el movimiento de una figura alrededor de un punto fijo llamado centro de rotación, con un ángulo de giro en sentido:
- Positivo: contrario a las manecillas del reloj.
- Negativo: en el mismo sentido de las manecillas del reloj.
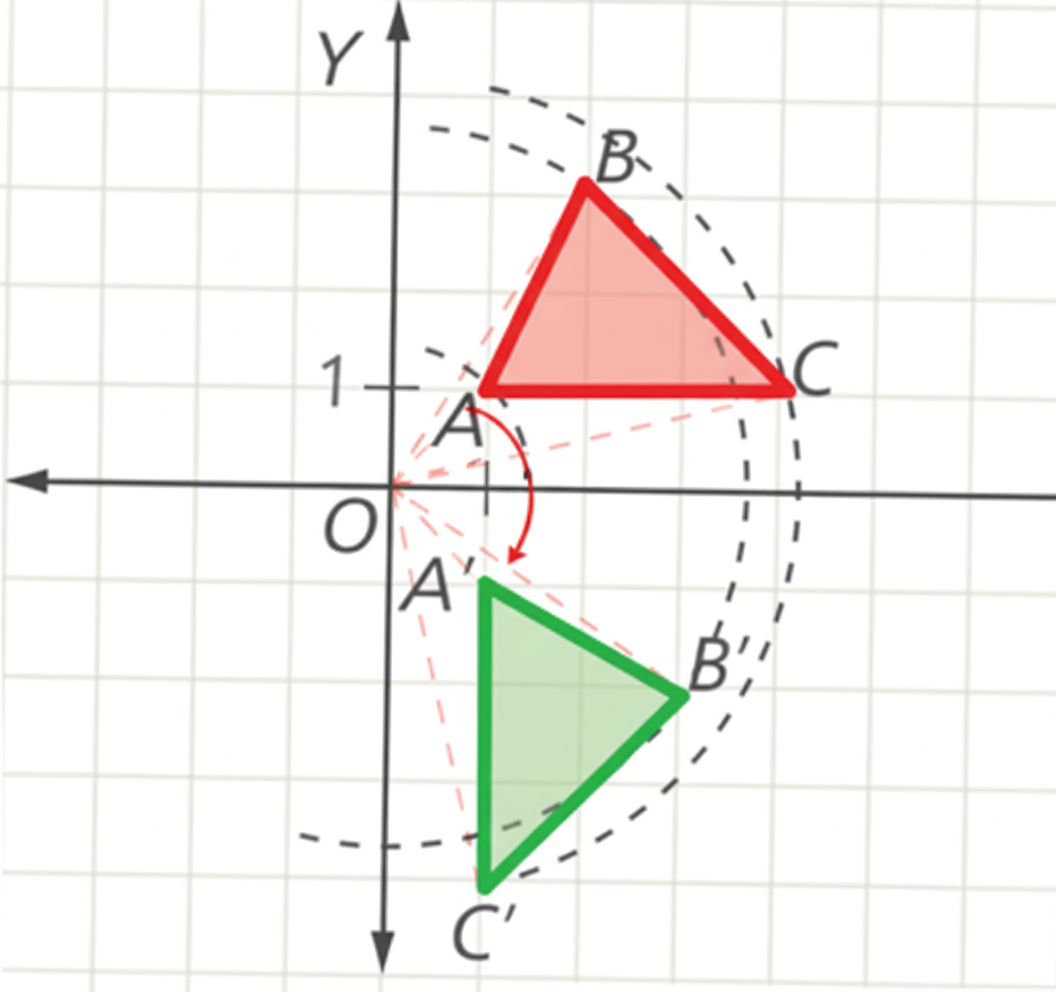
Ejemplo:
Un triángulo puede rotarse 90° alrededor del origen (0,0). En este caso, cada vértice gira en torno al centro de rotación manteniendo siempre la misma distancia respecto a él.
🔹 3. Reflexión
La reflexión es un movimiento que refleja una figura respecto a un eje (horizontal, vertical o diagonal).
- Cada punto de la figura se proyecta al otro lado del eje, a la misma distancia.
- El resultado es una “imagen en el espejo” de la figura original.
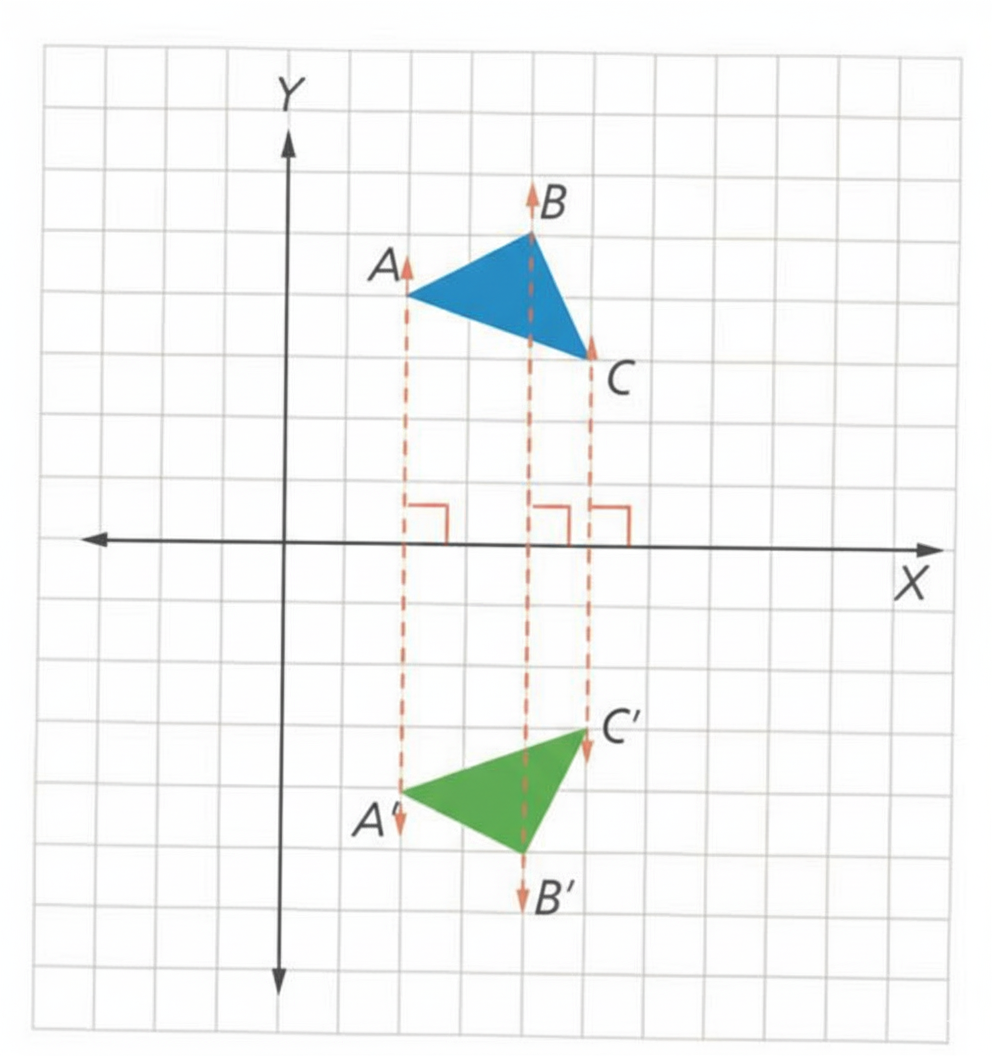
Ejemplo:
Un triángulo reflejado respecto al eje X se invierte verticalmente, obteniendo una figura congruente pero en posición opuesta.
🌟 Aplicaciones en la vida real
- Arte y decoración: los mosaicos y patrones en alfombras se logran mediante traslaciones y rotaciones.
- Tecnología: en diseño gráfico y animación, estos movimientos permiten crear simetrías y efectos visuales.
- Naturaleza: las alas de una mariposa son un claro ejemplo de reflexión.
✅ En conclusión, los movimientos en el plano son herramientas fundamentales para comprender la geometría y su relación con el mundo que nos rodea. Aprender a identificarlos y aplicarlos nos ayuda a desarrollar el pensamiento espacial, esencial en las matemáticas y en múltiples disciplinas.