¡Bienvenido! Hoy aprenderemos cómo realizar operaciones con fracciones de manera fácil y divertida. 🌟
Una fracción representa una parte de un todo, y está formada por:
- Numerador: el número de partes que tienes (arriba),
- Denominador: el número total de partes (abajo).
Por ejemplo, en \(\frac{2}{5}\), tenemos 2 partes de un total de 5.

Operaciones Básicas con Fraccionarios
➡️ 1. Suma y Resta de Fracciones
a) Fracciones con el mismo denominador
Cuando los denominadores son iguales, simplemente sumas o restas los numeradores:
- Ejemplo de suma: \(\frac{3}{7}\) + \(\frac{2}{7} \)= \(\frac{5}{7}\)
- Ejemplo de resta: \(\frac{5}{8} \)-\( \frac{1}{8}\) =\( \frac{4}{8}\) = \(\frac{1}{2}\)
Consejo: ¡Recuerda simplificar el resultado si es posible!
b) Fracciones con diferente denominador (Método de la «Carita Feliz») 😊
Cuando los denominadores son diferentes, podemos usar el divertido Método de la Carita Feliz:
¿Cómo funciona?
- Multiplica cruzado:
- El numerador de la primera fracción por el denominador de la segunda (arriba a la derecha).
- El numerador de la segunda fracción por el denominador de la primera (arriba a la izquierda).
- Multiplica los denominadores entre sí para el denominador común (abajo).
- Suma o resta los resultados de las multiplicaciones cruzadas.
🔵 Ejemplo de suma: \(\frac{2}{3} \)+ \(\frac{1}{4}\)
- Multiplicación cruzada:
- 2×4=8
- 1×3=3
- Suma:
- 8+3=11
- Multiplicación de denominadores:
- 3×4=12
- Resultado: \(\frac{11}{12}\)
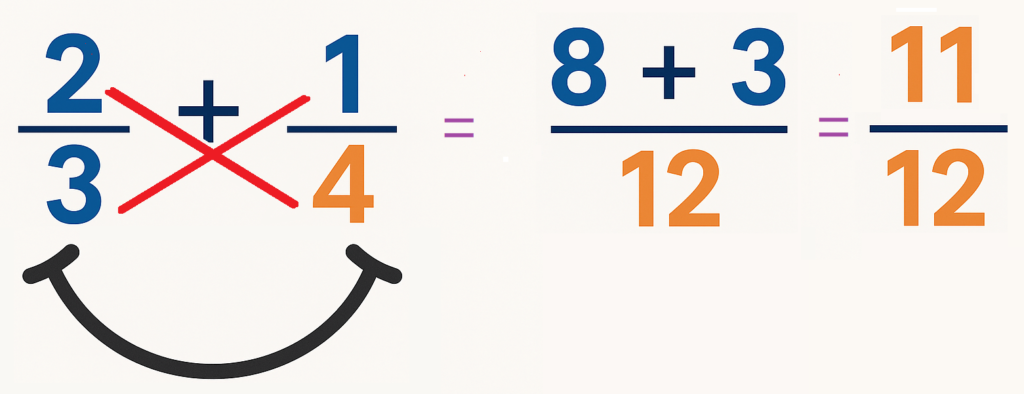
🔵 Ejemplo de resta: \(\frac{5}{6}\) – \( \frac{1}{4}\)
- Multiplicación cruzada:
- 5×4=20
- 1×6=6
- Resta:
- 20−6=14
- Multiplicación de denominadores:
- 6×4=24
- Resultado simplificado: \(\frac{14}{24} \)=\( \frac{7}{12}\)
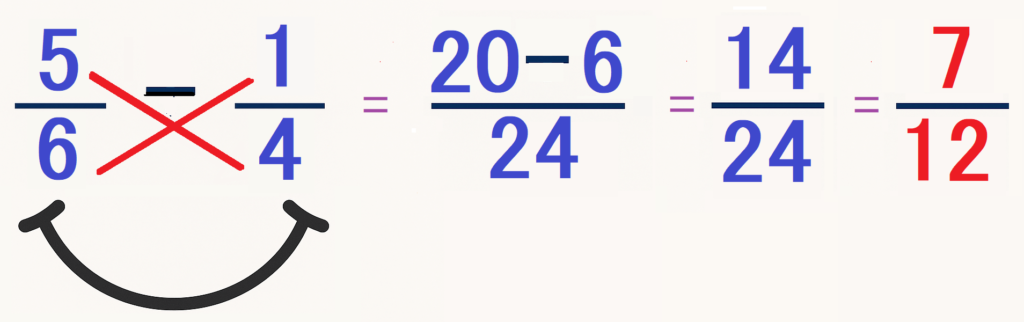
✨ Tip: Visualiza una carita: las líneas de las multiplicaciones cruzadas forman los ojos y la sonrisa.
➡️ 2. Multiplicación de Fracciones
Para multiplicar fracciones:
- Multiplica numerador por numerador,
- Multiplica denominador por denominador.
Ejemplo: \(\frac{2}{5} \times \frac{3}{4}\) = \(\frac{6}{20} \)=\( \frac{3}{10}\)
(Simplificando 6/20 por 2).
➡️ 3. División de Fracciones
Para dividir fracciones:
- Invierte la segunda fracción (intercambia numerador y denominador),
- Luego multiplica normalmente.
Ejemplo: \(\frac{3}{7} \div \frac{2}{5}\) = \(\frac{3}{7} \times \frac{5}{2}\) = \(\frac{15}{14}\)
¡Ahora te toca a ti!
Prueba estos ejercicios:
- \(\frac{1}{2} + \frac{1}{3}\)=
- \(\frac{5}{6} – \frac{1}{8}\)=
- \(\frac{4}{7} \times \frac{2}{5}\)=
- \(\frac{3}{4} \div \frac{2}{3}\)=
