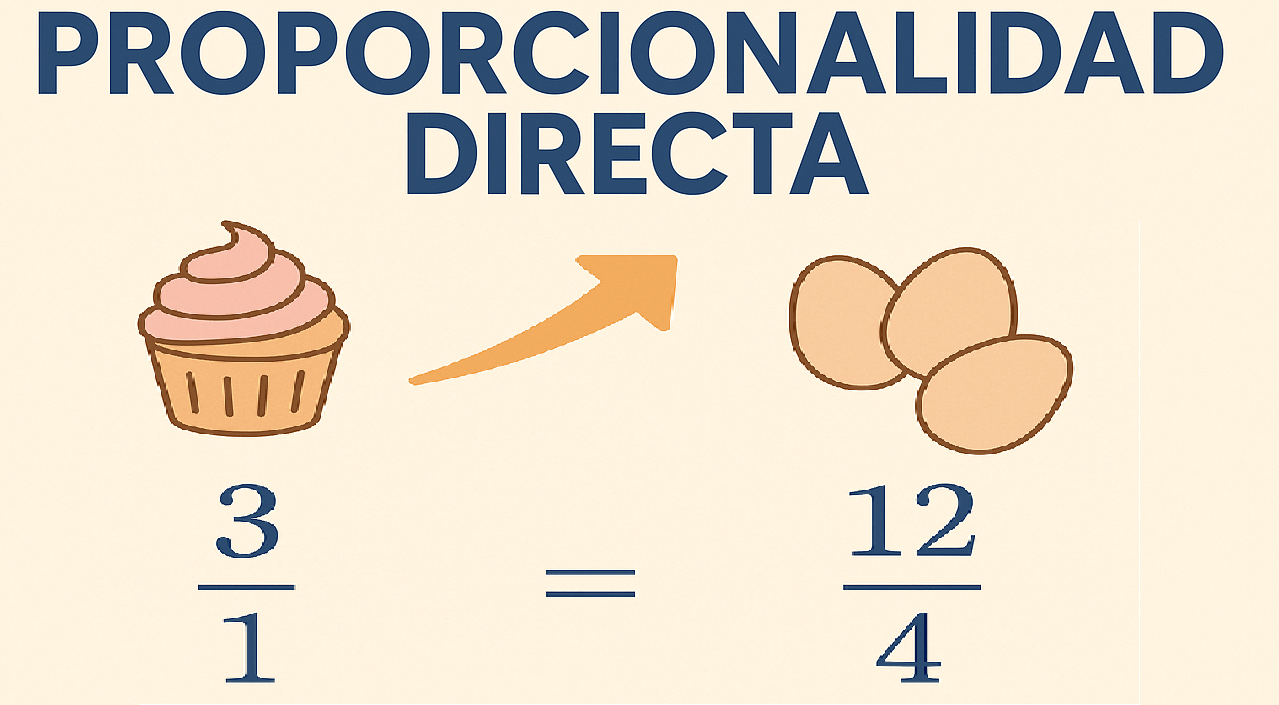
La proporcionalidad directa es una relación entre dos cantidades donde, si una aumenta, la otra también aumenta en la misma proporción.
🧠 ¿Qué significa esto?
Imagina que estás preparando postres y necesitas huevos. Si para hacer 1 postre usas 3 huevos, entonces:
- Para hacer 2 postres necesitarás 6 huevos
- Para 4 postres, 12 huevos
- Y para 7 postres, 21 huevos
Mira esta tabla:
| Número de postres | Número de huevos |
|---|---|
| 1 | 3 |
| 2 | 6 |
| 4 | 12 |
| 7 | 21 |
🧮 ¿Cómo sabemos que son proporcionales?
Si dividimos el número de huevos entre el número de postres, siempre obtenemos el mismo resultado:
\[ \frac{3}{1} = 3, \quad \frac{6}{2} = 3, \quad \frac{12}{4} = 3, \quad \frac{21}{7} = 3 \]
Esto nos muestra que las cantidades son directamente proporcionales porque el cociente es constante.
📌 Definición clave:
Dos magnitudes son directamente proporcionales si al aumentar una, la otra también aumenta manteniendo siempre el mismo cociente.
🧪 Ejemplo práctico:
Laura utilizó 3 huevos para preparar un postre.
¿Cuántos postres puede preparar con 12 huevos? ¿Cuántos huevos necesitará para preparar 7 postres? \(\frac{postre}{huevos} \frac{→}{→} \quad\frac{1}{3} = \frac{x}{12} \Rightarrow \)
\(x = \frac{12 · 1}{3} \Rightarrow \)
\(x = \frac{12 }{3} \Rightarrow \)
\(x =4\)\(\frac{postre}{huevos} \frac{→}{→}\quad \frac{1}{3} = \frac{7}{x} \Rightarrow \)
\(x = \frac{3 · 7}{1} \Rightarrow \)
\(x = \frac{21 }{1} \Rightarrow \)
\(x =21\)Puede preparar 4 postres. Necesita 21 huevos.
💡 Recuerda: cuando dos cantidades son directamente proporcionales, puedes usar regla de tres o una proporción para resolver cualquier problema fácilmente.