El volumen es la medida del espacio que ocupa un cuerpo en el espacio tridimensional. Se usa para calcular cuánto “caben” dentro de un objeto: aire, líquido, objetos sólidos, etc.
En el Sistema Internacional (SI), la unidad principal de volumen es el metro cúbico (m³), que corresponde al volumen de un cubo cuyos lados miden 1 metro.
🟨 1. El metro cúbico y sus múltiplos y submúltiplos
Así como ocurre con las unidades de longitud, el metro cúbico tiene múltiplos (más grandes) y submúltiplos (más pequeños):
| Unidad | Equivalencia |
|---|---|
| 1 km³ | 1 000 000 000 m³ |
| 1 hm³ | 1 000 000 m³ |
| 1 dam³ | 1 000 m³ |
| 1 m³ | unidad base |
| 1 dm³ | 0.001 m³ = 1 L |
| 1 cm³ | 0.000001 m³ |
| 1 mm³ | 0.000000001 m³ |
🔹 Dato útil:
1 dm³ = 1 litro (L)
1 cm³ = 1 mL
🟧 2. Cómo se forma un metro cúbico
Un cubo de 1 m de arista contiene:
- 1 000 dm³
- 1 000 000 cm³
- 1 000 000 000 mm³
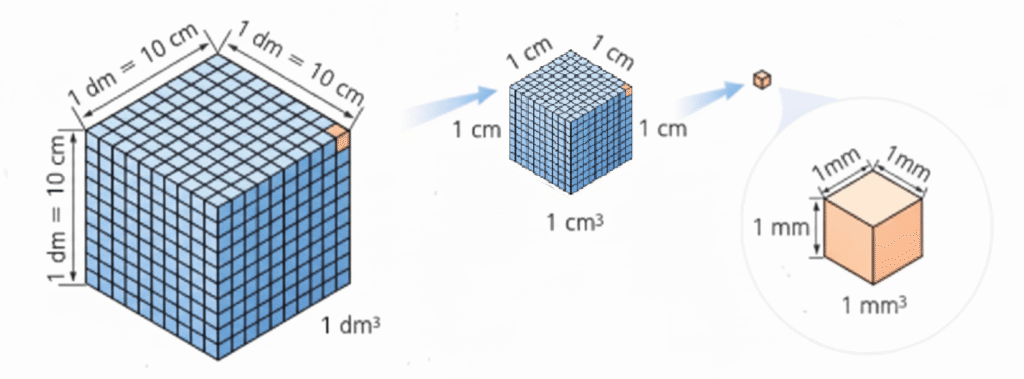
Por lo tanto:
\[
1\,\text{m}^3 = 10\,\text{dm}^3 \times 10\,\text{dm}^3 \times 10\,\text{dm}^3 = 1\,000\,\text{dm}^3
\]
\[
1\,\text{dm}^3 = 10\,\text{cm}^3 \times 10\,\text{cm}^3 \times 10\,\text{cm}^3 = 1\,000\,\text{cm}^3
\]
\[
1\,\text{cm}^3 = 10\,\text{mm}^3 \times 10\,\text{mm}^3 \times 10\,\text{mm}^3 = 1\,000\,\text{mm}^3
\]
🟩 3. Conversión entre unidades de volumen
Para convertir entre unidades, se multiplica o divide por 1000, porque el volumen crece en 3 dimensiones (10 × 10 × 10).
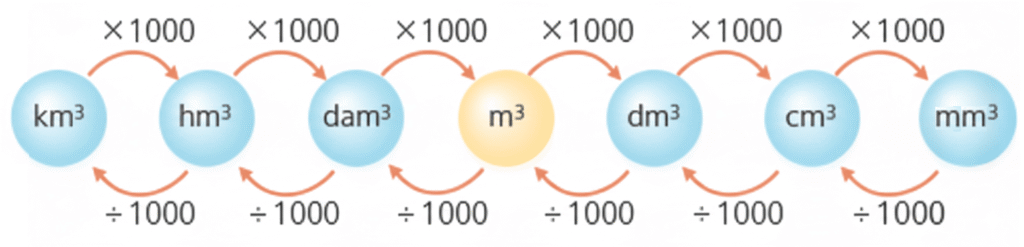
Ejemplo:
🔹 Convertir 34 000 cm³ en m³
\[
34000 \div 1000000 = 0.034\,\text{m}^3
\]
🔹 Convertir 6 hm³ a m³
\[
6\,\text{hm}^3 = 6 \times 1\,000\,000 = 6\,000\,000\,\text{m}^3
\]
🟦 4. Ejemplos de cubos y estructuras
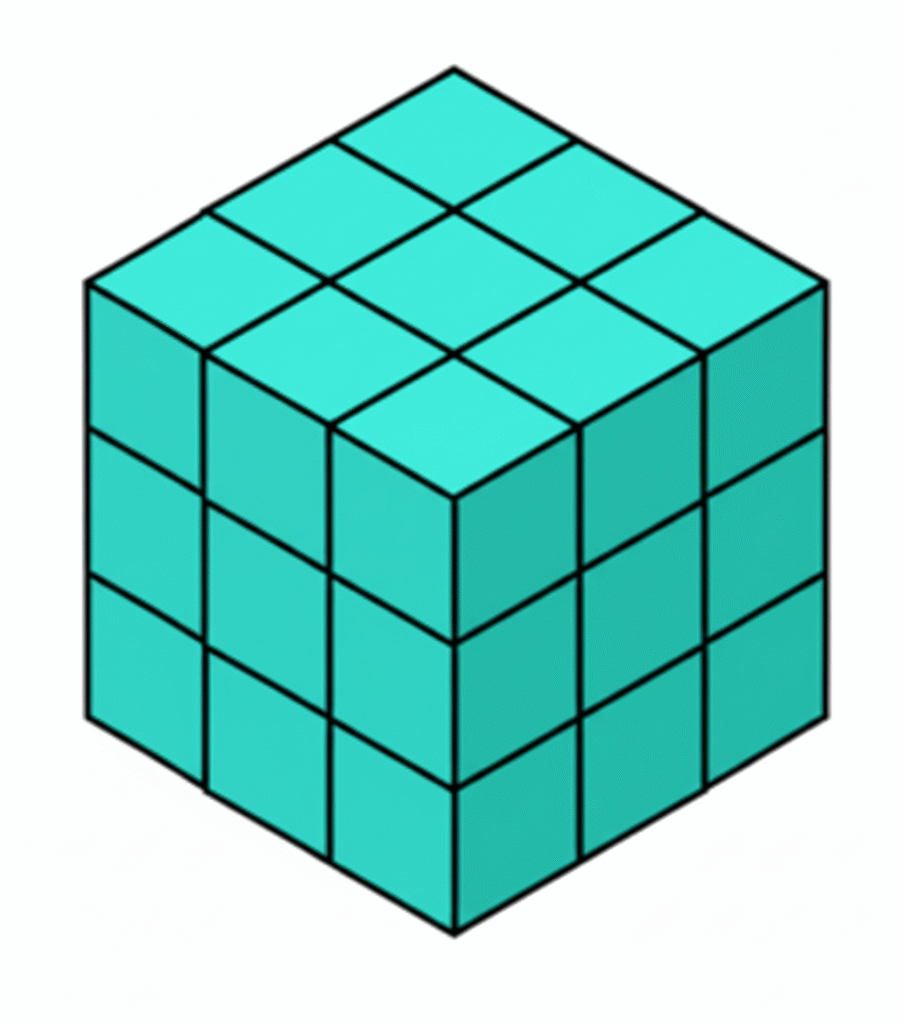
🔹 Ejemplo 1
Un obrero apila cajas formando un cubo de 3 cajas por lado. ¿Cuánta cajas amontonó el operario?
\[
3 \times 3 \times 3 = 27\ \text{cajas}
\]
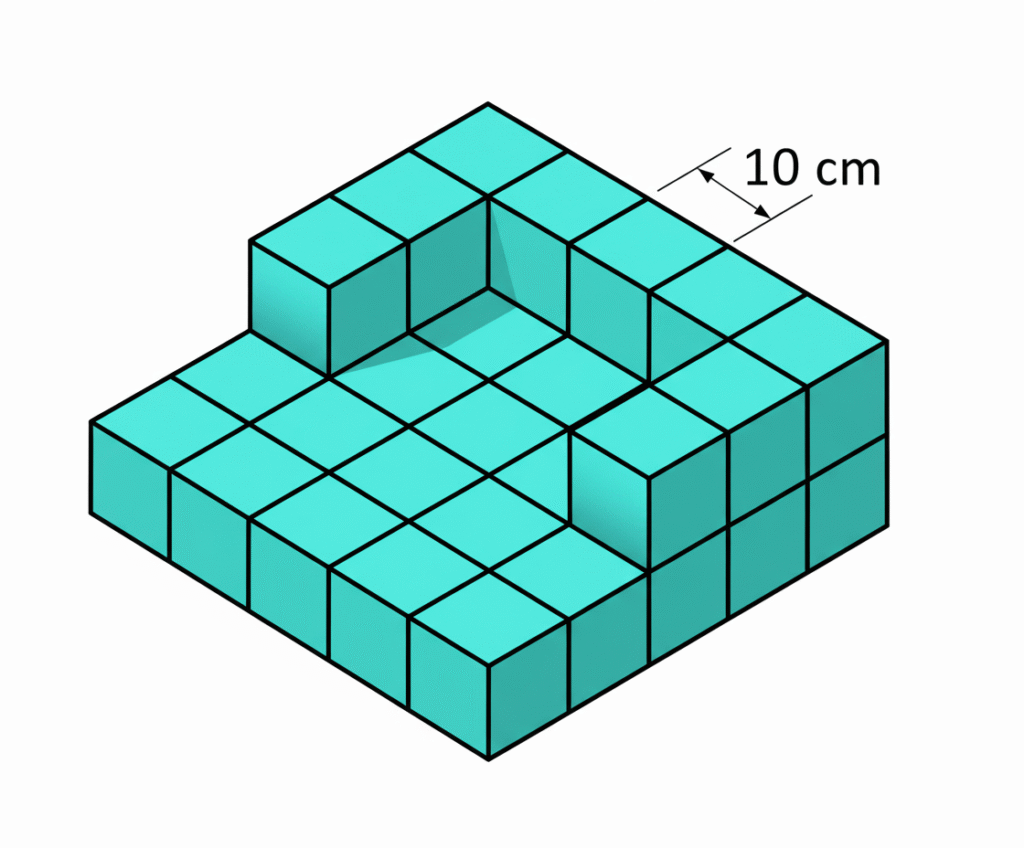
🔹 Ejemplo 2
Una estructura está formada por cubos de 10 cm de arista.
Cada cubo tiene volumen:
\[
10 \times 10 \times 10 = 1000\,\text{cm}^3
\]
Si la estructura contiene 34 cubos:
\[
34 \times 1000 = 34\,000\,\text{cm}^3
\]
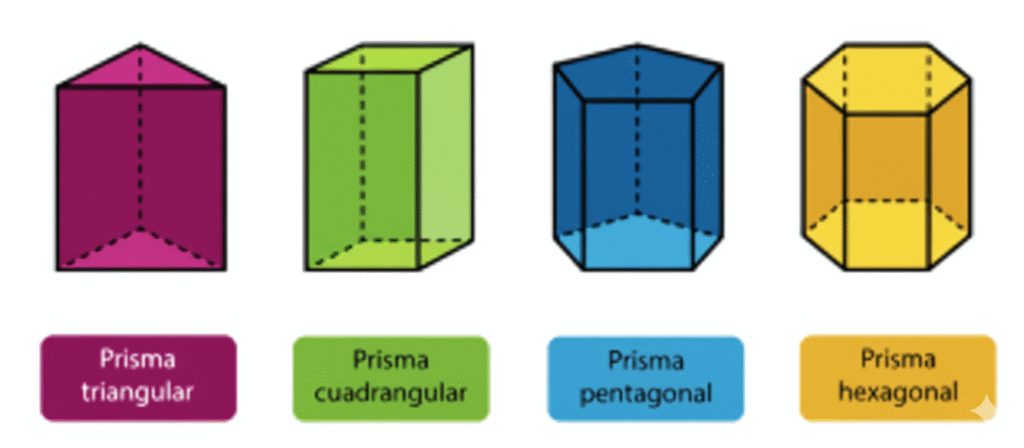
🟥 5. Volumen de prismas
Un prisma es un cuerpo geométrico con dos bases iguales y paralelas, unidas por caras laterales planas, que suelen ser rectángulos. Su nombre depende de la forma de su base, como un prisma cuadrangular si la base es un cuadrado, o un prisma triangular si la base tiene forma de triángulo. Es como una caja con dos tapas de la misma forma.
El volumen de un prisma se calcula multiplicando:
\[
\fbox{$V = A_{\text{base}} \times h$}
\]
Ejemplo:
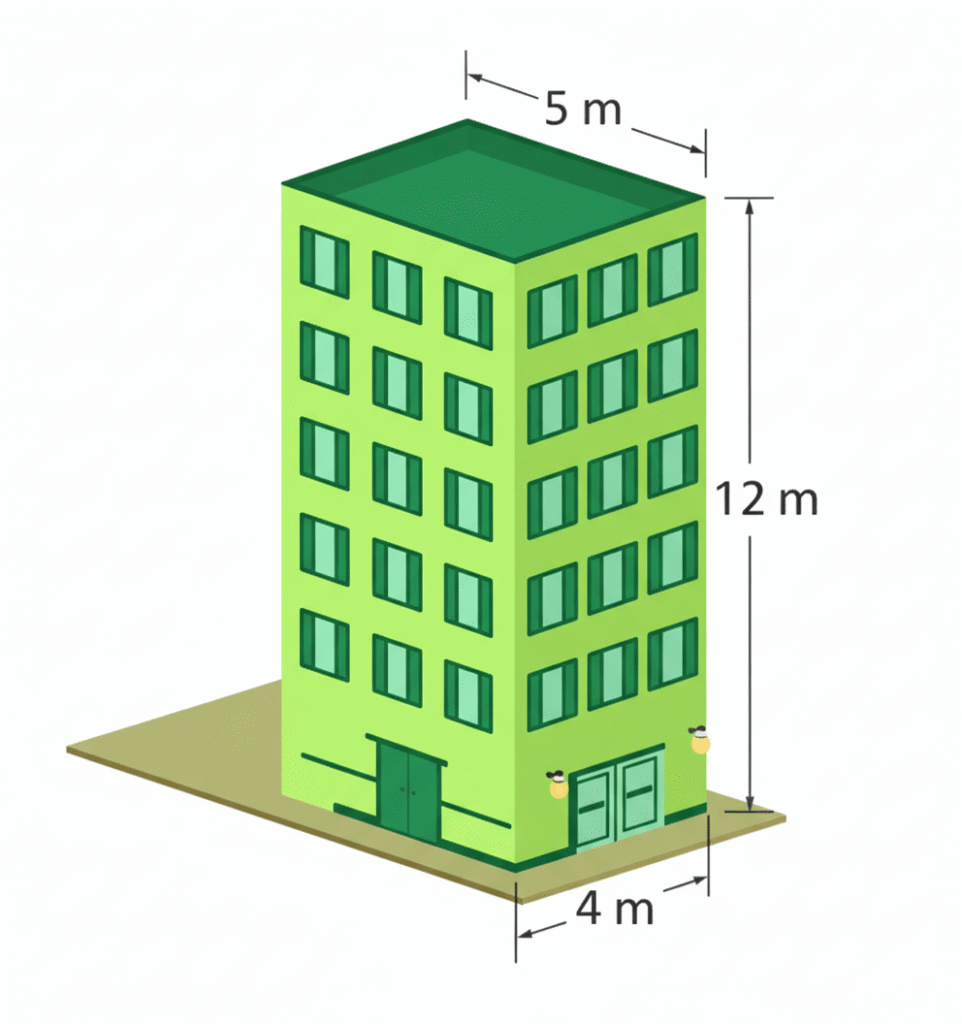
Hallar el volumen de un edificio de base de 4 m × 5 m y altura de 12 m.
\[
A_{\text{base}} = 4 \times 5 = 20\,\text{m}^2
\]
\[
V = 20 \times 12 = 240\,\text{m}^3
\]
🟪 6. Volumen de pirámides
Las pirámides son cuerpos geométricos tridimensionales con una base poligonal y caras laterales triangulares que se unen en un único vértice o cúspide.
El volumen de una pirámide es:
\[
\fbox{$V = \frac{A_{\text{base}} \times h}{3}$}
\]
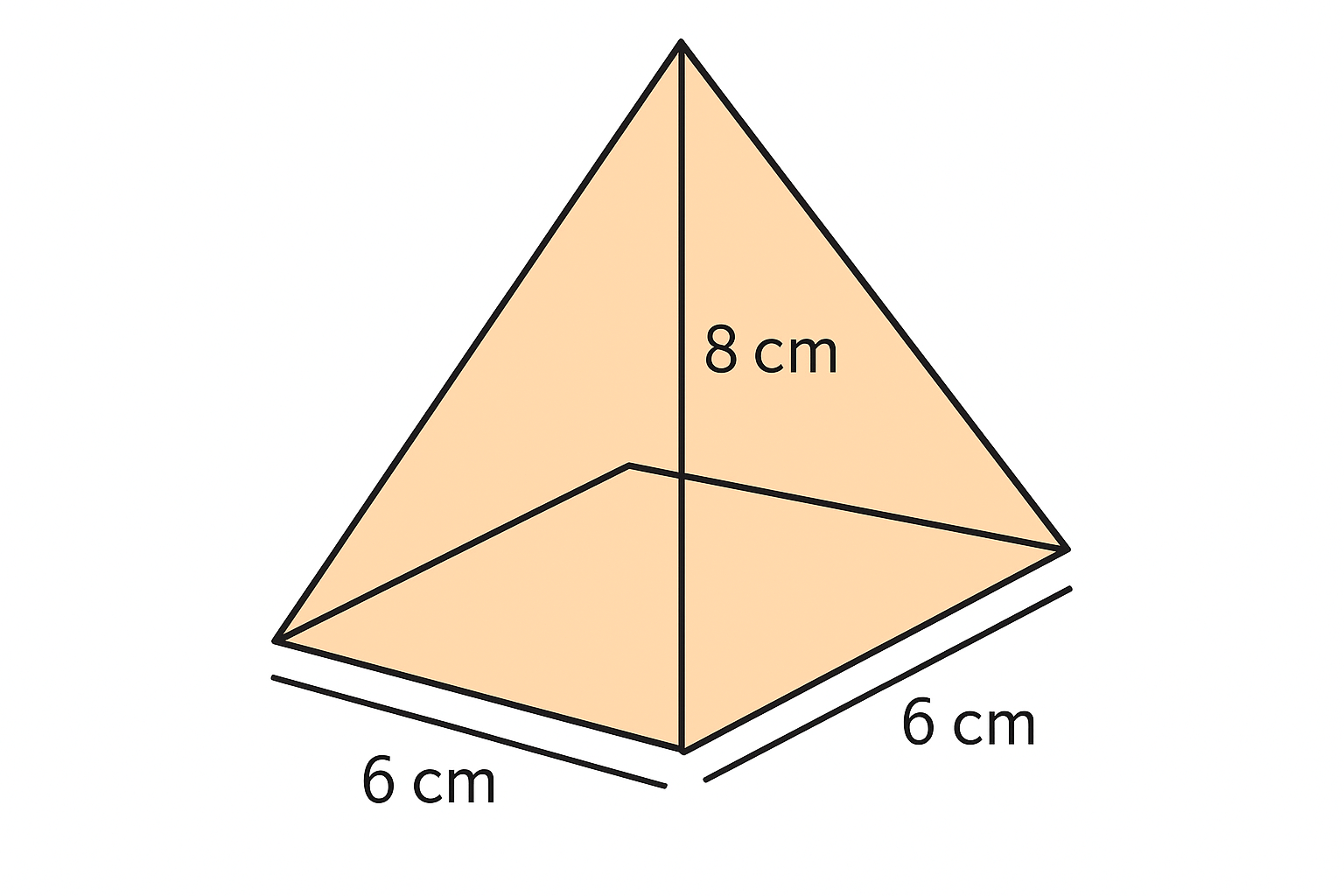
Ejemplo:
Base cuadrada de 6 cm × 6 cm
Altura: 8 cm
\[
A_{\text{base}} = 6 \times 6 = 36\,\text{cm}^2
\]
\[
V = \frac{36 \times 8}{3} = 96\,\text{cm}^3
\]
⭐ Conclusión
Las unidades de volumen permiten medir objetos tridimensionales. Recordar la relación entre unidades y practicar con cubos o prismas facilita la comprensión. Las conversiones siempre se hacen multiplicando o dividiendo por 1000.
